NCERT QUESTIONS
3.1: The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4Ω, what is the maximum current that can be drawn from the battery?
Solution :
Given that Emf of the battery, E = 12 V
The battery has an Internal resistance of R = 0.4 Ω
The Maximum current drawn from the battery is given by = I
According to Ohm’s law,
E = IR
I=E / R I=12/0.4 = 30 A
The maximum current drawn from the given battery is 30 A.
3.2: A battery of emf 10 V and internal resistance 3 Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?
Solution :Electromotive force (E) of battery = 10 volt.
Internal Resistance r of the battery = 3 Ω
Current in the Circuit (I) = 0.5 A
Let the resistance of the required resistor is R Ω
Let the Terminal voltage of the register be V.
As per Ω ’s law,
3.3: At room temperature (27.0 °C) the resistance of a heating element is 100Ω. What is the temperature of the element if the resistance is found to be 117Ω, given that the temperature coefficient of the material of the resistor is 1.70 × 10–4 °C–1.
Solution: Given: Temperature coefficient of filament,
α = 1.70 × 10-4 per °C
Let T1 be the temperature of element, R1 = 100Ω (Given: T1 = 27°C)
Let T2 be the temperature of element, R2 = 117Ω
To find T2 = ?
The formula is: R2 = R1[1 + α(T2-T1)]
⇒ R2 – R1 = R1α(T2 – T1)
⇒ R2 – R1 = R1α (T2 – T1)
3.4: A negligibly small current is passed through a wire of length 15 m and uniform cross-section 6.0 × 10–7 m2, and its resistance is measured to be 5.0 Ω. What is the resistivity of the material at the temperature of the experiment?
Solution:
Given that the length of the wire, L = 15 m
The area of cross-section is given as , a = 6.0 x 10 – 7 m 2
Let the resistance of the material of the wire be, R, i.e., R = 5.0 Ω
The resistivity of the material is given as ρ
.
3.5: A silver wire has a resistance of 2.1 Ω at 27.5 °C, and a resistance of 2.7 Ω at 100 °C. Determine the temperature coefficient of resistivity of silver.
Solution:
Given that temperature T1 = 27.5 ° C
Resistance R1 at temperature T1 is given as:
R1 = 2.1 Ω ( at T 1 )
Given that temperature T2 = 100 ° C
Resistance R2 at temperature T2 is given as:
R2 = 2.7 Ω ( at T 2 )
Temperature coefficient of resistivity of silver = α
The formula for α is: R2 = R1[1 + α(T2-T1)]
⇒ R2 – R1 = R1α(T2 – T1)
⇒ R2 – R1 = R1α (T2 – T1)
3.6: A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A, which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27.0 °C? The temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70 × 10–4°C–1.
Solution:
In the given problem,
The supply voltage, V = 230 V
The initial current drawn, I1 = 3.2 A
Consider the initial resistance to be R1, which can be found by the following relation: R1 = V/I
R1 = 230V/3.2A
R1 = 71.87 Ω
Steady value of current I2 = 2.8Ampere
Resistance R α is given by R2 = 230V/2.8A
R2 = 82.14 Ω
Temperature coefficient of nichrome wire α = 1.70 × 10-4 per °C
Initial temperature of nichrome T1 = 27 ° C
Steady Temperature attained by nichrome = T2
The formula is: R2 = R1[1 + α(T2-T1)]
⇒ R2 – R1 = R1α(T2 – T1)
⇒ R2 – R1 = R1α (T2 – T1)
3.7: Determine the current in each branch of the network shown in the figure:
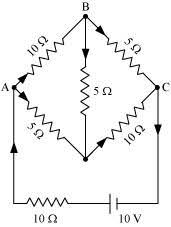
Solution :The current through the labelled diagram shows the current flowing the respective branches:
For the closed circuit ABDA, potential is zero i.e.,
10I2 + 5I4 − 5I3 = 0
2I2 + I4 −I3 = 0
I3 = 2I2 + I4 … (1)
For the closed circuit BCDB, potential is zero i.e.,
5(I2 − I4) − 10(I3 + I4) − 5I4 = 0
5I2 + 5I4 − 10I3 − 10I4 − 5I4 = 0
5I2 − 10I3 − 20I4 = 0
I2 = 2I3 + 4I4 … (2)
For the closed circuit ABCFEA, potential is zero i.e.,
−10 + 10 (I1) + 10(I2) + 5(I2 − I4) = 0
10 = 15I2 + 10I1 − 5I4
3I2 + 2I1 − I4 = 2 … (3)
From equations (1) and (2), we obtain
I3 = 2(2I3 + 4I4) + I4
I3 = 4I3 + 8I4 + I4
− 3I3 = 9I4
− 3I4 = + I3 … (4)
Putting equation (4) in equation (1), we obtain
I3 = 2I2 + I4
− 4I4 = 2I2
I2 = − 2I4 … (5)
It is evident from the given figure that,
I1 = I3 + I2 … (6)
Putting equation (6) in equation (1), we obtain
3I2 + 2(I3 + I2) − I4 = 2
5I2 + 2I3 − I4 = 2 … (7)
Putting equations (4) and (5) in equation (7), we obtain
5(−2 I4) + 2(− 3 I4) − I4 = 2
− 10I4 − 6I4 − I4 = 2
17I4 = − 2
I4 = -2/17Ampere
Equation (4) reduces to
I3 = − 3(I4)
I3 = -3 × -2/17
I3 = 6/17Ampere
I2 = -2(I4)
I2 = -2 × -2/17
I2 = 4/17Ampere
I2 – I4 = 6/17Ampere
I3 + I4 = 6/17Ampere
I1 = I2 + I3 = 4/17 + 6/17 = 10/17 Ampere
Therefore, current in branch AB = 4/17Ampere
In branch BC = 6/17Ampere
In branch CD = -4/17Ampere
In branch AD = 6/17Ampere
In branch BD = -2/17Ampere
Total current = 4/17 + 6/17 + -4/17 + 6/17 + -2/17 = 10/17 Ampere.
3.8: A storage battery of emf 8.0 V and internal resistance 0.5 Ω is being charged by a 120 V dc supply using a series resistor of 15.5 Ω. What is the terminal voltage of the battery during charging? What is the purpose of having a series resistor in the charging circuit?
Solution :
Electromotive force EMF of battery = 8Volt
Internal resistance of battery r = 0.5 Ω
Supply Voltage V = 120Volt
Resistance of resistor R = 15.5 Ω
Effective voltage in circuit = V1
Since Resistance R is connected in series, we can write V1 = V-E
V1 = 120V-8V = 112 V
Current flowing in the circuit:
.
3.9: The number density of free electrons in a copper conductor estimated in Example 3.1 is 8.5 × 1028 m–3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10–6m2 and it is carrying a current of 3.0 A.
Solution: Given that Number density of free electrons in a copper conductor, n = 8.5 x 10 28 m – 3
Let the Length of the copper wire be l
Given , l = 3.0 m
Let the area of the cross-section of the wire be A = 2.0 x 10 – 6 m 2
The value of the current carried by the wire, I = 3.0 A, which is given by the equation,
I = n A e V d
Where,
e = electric charge = 1.6 x 10 – 19 C
