NCERT QUESTIONS
2.1: Two charges 5 × 10-8 C and -3 x 10-8 C are located 16 cm apart from each other. At what point (s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Solution :
Given,
Two charges qA = 5 x 10-8 C and qB = -3×10-8 C
Distance between two charges, r = 16 cm = 0.16 m
Consider a point O on the line joining two charges where the electric potential is zero due to two charges.
2.2: A regular hexagon of side 10 cm has a charge of 5 µC at each of its vertices. Calculate the potential at the centre of the hexagon.
Solution: Let O be the center of the hexagon. It contains the charges at all its 6 vertices; each charge = + 5 μC = 5×10-6 C. The side of the hexagon is 10 cm = 0.1 m
It follows that the point O, when joined to the two ends of a side of the hexagon, forms an equilateral triangle. Electric potential at O due to one charge,
2.3: Two charges of 2 μC and −2 µC are placed at points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Solution :
(a) For the given system of two charges, the equipotential surface will be a plane normal to the line AB joining the two charges and passing through its mid-point O. On any point on this plane, the potential is zero.
(b) The electric field is in a direction from point A to point B, i.e., from the positive charge to the negative charge and normal to the equipotential surface.
2. 4: A spherical conductor of radius 12 cm has a charge of 1.6 × 10-7 C distributed uniformly on its surface. What is the electric field?
(a) Inside the sphere
(b) Just outside the sphere
(c) At a point 18 cm from the centre of the sphere?
Solution: Given, q = 1.6 x 10-7 C
Radius of the sphere, r = 12 cm = 0.12 m
(a) The charge is evenly distributed across the conductor. The electric field within a spherical conductor is zero because the total net charge within a conductor is zero.
(b) Just outside the sphere: For a point on the charged spherical conductor or outside it, the charge may be assumed to be concentrated at its center.
2. 5: A parallel plate capacitor with air between the plates has a capacitance of 8 pF (1 pF = 10-12 F). What will be the capacitance if the distance between the plates is reduced by half and the space between them is filled with a substance of dielectric constant 6?
Solution :Given: Capacitance of capacitor when medium between two plates is air, C = 8 pF = 8×10–12 F
2. 6: Three capacitors, each of capacitance 9 pF, are connected in series.
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
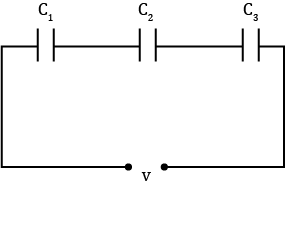
Solution :Given, C1 = C2 = C3 = 9 pF = 9 x 10-12 F
V = 120 volt
.
2. 7: Three capacitors of capacitances 2 pF, 3 pF, and 4 pF are connected in parallel.
(a) What is the total capacitance of the combination?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
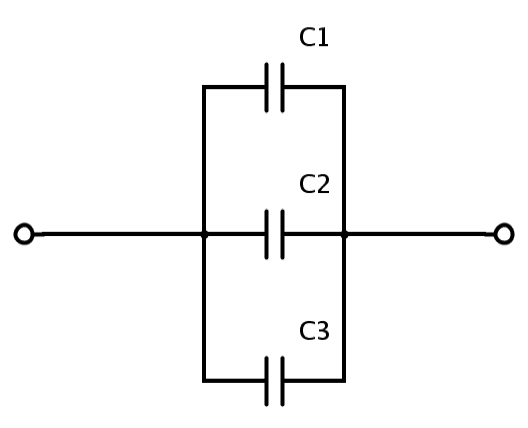
Solution :
(a) The capacitances of the given capacitors are, C1=2pF; C2=3pF; C3=4pF
The equivalent capacitance ( C) of the parallel combination is given by
C=C1+C2+C3
⇒C′=2+3+4 = 9pF
Therefore, the total capacitance of the combination is 9 pF.
Supply voltage, V = 100 V
(b) Let q1 , q2 and q3 be that charges on the capacitor C1 , C2 and C3 respectively.
In the parallel combination the potential difference across each capacitor will be equal to the supply voltage i.e., 100 V
⇒ q1 = C1V = 2 x 10-12×100 = 2× 10-10 C
⇒ q2 = C2V = 3 x 10-12×100 = 3× 10-10 C
⇒ q3 = C3V = 4 x 10-12×100 = 4× 10-10 C
2.8: In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10-3 m2 and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Solution : Area of each plate, A = 6 x 10-3 m2
Distance between the plates, d = 3mm = 3 X 10-3 m
Supply voltage, V = 100 V
As Capacitance C = 17.71 x 10-12 F = 17.71 pF.
As, q = CV = 17.71 x 10-12 x 100 = 17.71 x 10-10 C = 1.771 x 10-9 C.
2.9: Explain what would happen if in the capacitor given in Exercise 2.8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates.
(a) While the voltage supply remained connected.
(b) After the supply was disconnected.
Solution : (a) When the voltage supply remains connected:
The capacitance of the capacitor will become K times.
Therefore, C’ = kC
Where k = dielectric constant = 6×17.7pF = 106.2 pF
The potential difference across the two plates of the capacitor will remain equal to the supply voltage i.e. 100 V
The charge on the capacitor,
q’ = C’V = 160.2 x 10-12 x 100
= 1.602 x 10-8 C
(b) After the voltage supply is disconnected:
As calculated above, the capacitance of the capacitor, C’ = 106.2 pF
The potential difference will decrease on introducing mica sheet by a factor of K,
2.10: A 12 pF capacitor is connected to a 50V battery. How much electrostatic energy is stored in the capacitor?
Solution: Given, C = 12 pF = 12 x 10-12 F
V = 50 V
The electrostatic energy stored in the capacitor,
W = (½) CV2 = (½) × 12 × 10-12× (50)2 = 1.5 × 10-8 J
2.11: A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Solution: Given, C1 = 600 pF = 600 x 10-12 F
V1 = 200 V
Energy stored in the capacitor,
U1 = (½) C1 (V1)2 = (½)×600× 10-12× (200)2
= 12×10-6 J
When this charged capacitor is connected to another uncharged capacitor C2 ( = 600 pF) ,they will share charges, till potential differences across their plates become equal.
Total charge on the two capacitors,
q = C1V1 + C2V2 = 600 × 10-12× 200 + 0
= 12 ×10-8 C
Total capacitance of the two capacitors,
C = C1 + C2 = 600 pF + 600 pF
= 1200 pF
= 1200 x 10-12 F
